そもそも面積とは、「その図形が平面上でどれくらいの広さを占めているか」を数で表したものです 。 「公式を覚える」前に、次のシンプルな考え方を知っておくと、計算がとても得意になりますので覚えておきましょう 。
- 「1cm×1cmの小さな正方形」が何個分入るかという考え方が、すべての基本
- たとえば、その1cm×1cmの小さな正方形が40個分入るなら面積は、40cm²
- 円の場合でも考え方は同じ
- どんなに複雑な形に見えても、切り取ったり動かしたりして形を変えれば、最後は長方形と同じように計算できる
この記事は、主に小学校4年生、5年生、6年生が学ぶ平面図形の面積の求め方をわかりやすく解説しています。
小学生の皆さんが面積の求め方を理解して、もっともっと、算数が好きになってもらえるきっかけになれば幸いです。
目次
図形ごとの公式(魔法の合言葉)
それぞれの図形の面積を出す公式をまとめました。
長方形
「たて × よこ」を計算すると面積がわかります。小さな正方形が「何行 × 何列」並んでいるかを表しています 。

【問題】たての長さが5cm、よこの長さが8cm の長方形の面積を求めてみましょう 。
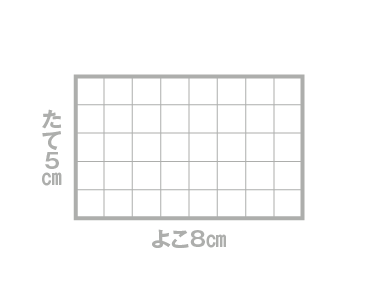
1. まずは「イメージ」してみましょう
たての長さが5cmなので、正方形がたてに5個並びます。よこの長さが 8cmなので、それがよこに8列分あります。つまり、「5個ずつの列が、8列分ある」という状態をイメージしてください。
2. 式を立てて計算します
長方形の面積は、「たて × よこ」で求められます 。
計算:5 × 8 = 40
3. 答えと確認
【答え】40cm²
単に数字を掛けるだけでなく、「正方形が全部で40個並んでいるんだな」と納得できると、公式がもっと身近になりますね 。
正方形
「一辺 × 一辺」を計算すると面積がわかります。たてとよこが同じ長さの、特別な長方形だと考えれば大丈夫です 。

平行四辺形
「底辺 × 高さ」を計算すると面積がわかります。端の三角形を切り取って反対側へ移すと、長方形に変わります 。

三角形
「底辺 × 高さ ÷ 2」を計算すると面積がわかります。同じ三角形を2つ合わせると平行四辺形になるので、それを半分にします 。

【問題】底辺が6cm、高さが4cmの三角形の面積を求めてみましょう。
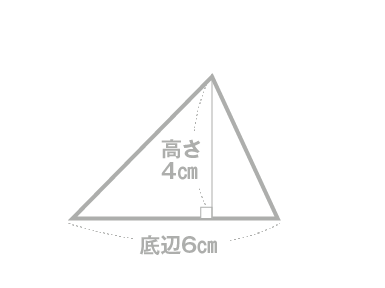
1. まずは「イメージ」してみましょう
三角形の面積を考えるときは、同じ形の三角形をもう1つ用意して、逆さまに組み合わせてみてください。 2つ合わせると、底辺6cm、高さ4cmの「平行四辺形」に変身します。 平行四辺形の面積は「底辺 × 高さ」で出せますが、求めたいのはその半分の三角形1つ分です。だから、最後に「÷ 2」を忘れないことがとても大切です。
2. 式を立てて計算します
三角形の面積は、「底辺 × 高さ ÷ 2」で求められます。
計算:6 × 4 ÷ 2
- ステップ①: まずは「底辺 × 高さ」を計算して、2つ分の面積を出します。 6 ÷ 4 = 24
- ステップ②: それを半分(÷ 2)にします。24 ÷ 2 = 12
3. 答えと確認
【答え】 12cm²
「どうして2で割るのかな?」という理由がわかれば、公式を忘れにくくなりますし、自信を持って答えを書けますね。
台形
「(上底+下底) × 高さ ÷ 2」を計算すると面積がわかります。同じ台形を逆さまにつなげると平行四辺形になり、その底辺が(上底+下底)になります 。

ひし形
「対角線 × 対角線 ÷ 2」を計算すると面積がわかります。対角線で分けると、全体の面積が長方形の半分として計算しやすくなります 。

円
「半径 × 半径 × 円周率」を計算すると面積がわかります。円周率は3.14など、問題の指示に合わせて使い分けましょう 。

【問題】半径が 4cm の円の面積を求めてみましょう。(円周率は 3.14 として計算してください)

1. まずは「イメージ」してみましょう
面積を「半径×半径×3.14」という呪文だけで覚える前に、図で考えてみます。
円の場合でも、1cm×1cmの小さな正方形が何個入るか、という考え方が活かせるので試してみましょう。半径が4cmなので、「4cm×4cmの正方形」を思い浮かべてください。この正方形の面積は16cm² ですね。円の面積は、この正方形が およそ 3.14個分 集まった広さになります。
2. 式を立てて計算します
公式にあてはめて計算を進めます。
計算:4×4×3.14
- ステップ①: まずは「半径 × 半径」を計算します。 4 × 4 = 16
- ステップ②: 次に、その結果に 3.14 を掛けます。 16 × 3.14 = 50.24
3. 答えと確認
【答え】50.24cm²
計算が終わったら、最初にした「イメージ」と比べてみましょう。 正方形1個分が 16cm² なので、その3倍(16 × 3 = 48)に近い数字になっていますね。このように、「だいたいこれくらいの大きさになるはずだ」と見当をつけることで、大きな計算ミスを防ぐことができます。
ここでミスしやすい!注意ポイント
テストで間違いやすい「2つの落とし穴」には気をつけましょう 。
「高さ」はまっすぐ(垂直)なところ!
平行四辺形、三角形、台形では、「ななめの辺」を高さとして使ってはいけません 。
- 高さとは、底辺に対して直角(90度)に引かれた線の長さのことです 。
- 図の中に「直角のマーク(∟)」がある場所を探すのが正解への近道です 。
「単位」をそろえましょう!
長さの単位がバラバラなときは、計算を始める前にそろえる必要があります 。
- たとえば「長さがm」で「面積がcm²」など、単位が混ざっていると正しい答えが出ません 。
- また、1m²は100cm²ではなく、10,000cm²(100cm×100cm)になる点も、間違いやすいので注意が必要です 。
「円」の計算は注意点がいっぱい!
- 問題に「直径」が書いてある場合は、必ず半分にして「半径」を求めてから計算しましょう。直径をそのまま公式に入れてしまうと、答えが4倍もズレてしまいます 。
- 先に「半径×半径」の計算を済ませてから、最後に3.14を掛けると、式がスッキリして計算ミスが減りますよ。
難しい形はどうすればいい?
カクカクしていたり、一部が丸くなってるような、いびつな面積の形が出てきたら、3つの作戦を使い分けましょう 。
- 分けてたす: 線を引いて、自分が知っている図形(長方形や三角形)に切り分けます 。
- 大きい形からひく: 大きな長方形などから、欠けている部分の面積を「くり抜く」ように引きます 。
- 動かす: 形の一部を切って別の場所へ移動させ、公式が使えるシンプルな形に変えます 。
まずは、基本の「たて×よこ」の計算と単位の書き方を確実にマスターすることから始めてみてくださいね!
まとめ
平面図形の面積の求め方の解説でしたが、いかがでしたでしょうか?「わかった!」という方もいれば、「やっぱりよくわからない・・・」という方もいると思います。
安心してください。今はわからなくても、基本の問題からコツコツ解いていけば、必ずできるようになりますよ!
算数以外の勉強方法や、受験対策には以下の記事も参考にしてみてください。
小学生が後悔しない塾の選び方ランキング! 塾選びで失敗しないためのポイントは?【お悩み診断付き】







